Abstract and Contents

6. Discussion

We presented an algorithm for the computation of the two-dimensional unstable manifold of a normally hyperbolic invariant circle or a hyperbolic fixed point of a three-dimensional diffeomorphism. Its main feature is the use of a linear foliation to assure the quality of the mesh on the unstable manifold. Because of normal hyperbolicity it is always possible to find a linear foliation that is transverse to 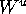in a neighborhood of the invariant circle or fixed point. If this foliation is also transverse to all of 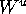the Foliation Condition is satisfied. This means that the complete unique intersection curve in each leaf can be computed. If the Foliation Condition is not satisfied the algorithm computes until an extra branch in one of the leaves is missed. In any case, a first piece of the unstable manifold is caclulated that contains .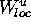

To find the intersection curve of 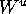with a leaf we compute a sequence of points by taking -steps along this curve. We remark that this idea can also be used to globalize the one-dimensional unstable manifold of a hyperbolic fixed point as a curve. The only difference is that the inverse image of a new point along the unstable manifold lies in the already computed piece of the curve (and not in a different leaf).

The Foliation Condition is in fact a condition on the global nature of 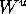: the unstable manifold may fold, but not in such a way that it becomes tangent to a suitable linear foliation; see Figure 18. Although we found several interesting examples of unstable manifolds that satisfy the Foliation Condition, this condition restricts the class of maps for which our algorithm can be used; see Section 5.4. The algorithm presented here should be considered as a first step. A promising idea for a general algorithm, using the fact that 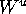is an immersed manifold, is the following. It is crucial that in each leaf there is a unique branch of the intersection curve of 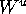in a -neighorhood of the farthest point. This is a local condition that is satisfied if we impose the Foliation Condition. In the future we plan to work with a local moving foliation that changes at each step and is perpendicular to the circle added last.

It is possible to adjust the algorithm so that it can be used to compute two-dimensional unstable manifolds in systems of dimension higher than three. The computation of unstable manifolds of dimension higher than two is much more complicated, and also requires the solution of serious problems concerning data management and visualization.

In the immediate future we intend to allow for steps of different sizes in different leaves. This is necessary in the special case that the unstable manifold is bounded. Consider a two-dimensional bounded unstable manifold 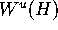of a normally hyperbolic invariant circle H that converges to an attracting invariant circle. The present algorithm computes a growing ring of 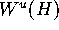with the same arclength distance from H in each leaf. The algorithm stops when the attractor is reached in one leaf, which means that, in general, a piece of the compact manifold 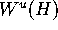is missed. The solution is to monitor the distance from the attractor in each leaf, and to adjust the step-size along the intersection curve with 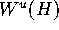accordingly.

All algorithms that compute a two-dimensional unstable manifold, with the exception of [Dellnitz and Hohmann 1996], are for vector fields; we refer to
[Guckenheimer and Worfolk 1993, Worfolk 1997, Johnson et al. 1995]. A vector field can be seen as a one-parameter family of time t maps. It is possible to use our algorithm for finding a two-dimensional unstable manifold of a vector field by considering the time 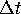map for a fixed 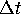. However, the algorithms for vector fields are better suited for this task; see also Section 5.4. Note that for a vector field, information about tangents is available that can be used to move in a prescribed direction. Furthermore, the integration time may be varied during the computation. Both is not possible for a single, fixed time 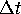map. The strength of our algorithm for the study of vector fields lies in considering Poincaré maps. As was demonstrated in Section 5.5, it allows to compute the three-dimensional unstable manifold of a periodic orbit or an invariant torus of a four-dimensional vector field.

Abstract and Contents

Written by: Bernd Krauskopf & Hinke Osinga
Created: May 27 1997 --- Last modified: Fri May 30 19:55:55 1997