![[HOME]](allfigs/logo.gif){kind=logo}
Abstract and Contents
Abstract and ContentsIn the case of a periodic vector field, a three-dimensional stable or unstable manifold can be computed as a two-dimensional manifold of the associated Poincaré map. This is demonstrated here with the three-dimensional stable and unstable manifolds of an invariant torus. The vector field under consideration is the normal form of a double Hopf bifurcation without resonance. Up to third order, the system is given in toroidal coordinates as
where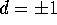 
and 
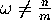for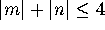 
. The unfolding is discussed in
[Guckenheimer and Holmes 1983,
Chow et al. 1994]. Throughout this
section we fix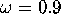 
, 
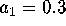and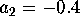 
.
For b = 2, c = 1 and d = -1, an invariant torus of saddle-type
exists in (8) in the entire
region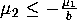 
and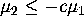 
. Hence, by taking 
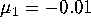and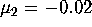 
, the associated Poincaré map defined on
the section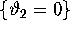 
has an invariant circle with both a
stable and an unstable normal direction. The circle is found by
solving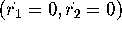 
. The linear approximation
of its stable and unstable manifolds is given by the eigenvectors of
this two-dimensional system times the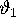 
-axis.
Starting at distance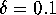 
on the linear approximation, we
compute the stable and the unstable manifolds. We use 50 mesh points
on the circle, and maintain a maximal distance of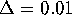 
between neighboring points. For the bisection error we take 
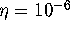. The Poincaré map is obtained by integration
of (8) with the fourth-order
Runge-Kutta method
from [Press et al. 1992].
The result is shown in Figure 17; the colored bands in
this picture have width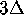 
, except for the part of the
unstable manifold that converges to the circle at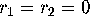 
. For
this part a 
-step is too large and the size of each ring is
equal to the minimal distance of the inner boundary of this ring to
its f-image. In
[Guckenheimer and Holmes 1983,
Chow et al. 1994] the stable and unstable manifolds are
qualitatively sketched in the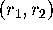 
-plane for 
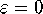. The
invariant torus of the vector field is then a fixed point. One branch
of the unstable manifold of this fixed point converges to the origin,
which is another fixed point. The two branches of the stable manifold
are asymptotic to the 
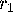- and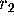 
-axis, respectively. In 
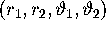-space, both fixed points are invariant
tori. Hence, one branch of the unstable manifold of the circle
converges to the invariant circle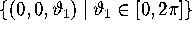 
. The branches of the stable manifold are
symptotic to the 
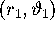- and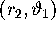 
-plane,
respectively. Note that due to the special form of
(8) the manifolds are linear in
the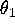 
direction.
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 19:55:22 1997
