![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and ContentsIf the Foliation Condition is not satisfied, it is still possible to compute part of the global manifold. This is illustrated with the computation of the stable manifold of the origin for the Lorenz system
We use the standard choice 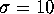 ,
, 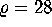 and
and 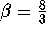 for the parameters. The stable manifold of the origin is
known to have a complicated structure, because it wraps in between the
well-known Lorenz attractor, which is located around two other
equilibria. As a consequence,
for the parameters. The stable manifold of the origin is
known to have a complicated structure, because it wraps in between the
well-known Lorenz attractor, which is located around two other
equilibria. As a consequence, 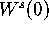 spirals around the z-axis. It
is best to use an algorithm designed for vector fields to compute
spirals around the z-axis. It
is best to use an algorithm designed for vector fields to compute
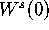 ,
like it was done to obtain Figure 15,
produced by [Worfolk 1997].
,
like it was done to obtain Figure 15,
produced by [Worfolk 1997].
Nevertheless, we demonstrate with the computation of this manifold how
our algorithm performs when the Foliation Condition is not
satisfied. To this end we consider the time t map
of (7) for fixed 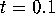 , where a fourth-order
Runge-Kutta method is used for the integration;
see [Press et al. 1992]. We take the linear foliation
, where a fourth-order
Runge-Kutta method is used for the integration;
see [Press et al. 1992]. We take the linear foliation
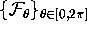 , where
, where 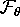 is the plane
perpendicular to
is the plane
perpendicular to 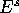 , through the ray in
, through the ray in 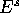 with argument
with argument
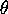 . Note that
. Note that 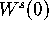 is such that any linear foliation
violates the Foliation Condition. The result of the computation is
shown in Figure 16.
is such that any linear foliation
violates the Foliation Condition. The result of the computation is
shown in Figure 16.
The intersections of 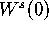 with leaves of
with leaves of 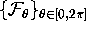 are computed with an accuracy of
are computed with an accuracy of
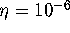 . The first ring is
centered at the origin and has inner radius
. The first ring is
centered at the origin and has inner radius
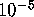 and outer
radius
and outer
radius 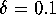 . On each boundary of the ring we take 40
uniformly spaced mesh points. The width of the rings on the manifold
does not exceed
. On each boundary of the ring we take 40
uniformly spaced mesh points. The width of the rings on the manifold
does not exceed 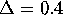 , and the colored rings in
Figure 16 have width
, and the colored rings in
Figure 16 have width 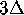 . If the distance between
neighboring points on different leaves exceeds
. If the distance between
neighboring points on different leaves exceeds 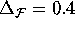 , an additional leaf is added. We repeated the computation with
smaller
, an additional leaf is added. We repeated the computation with
smaller  and
and 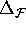 , but the result was
similar. The manifold in
Figure 16
does not seem to intersect
the attractor, which is another indication that our computation is
correct.
, but the result was
similar. The manifold in
Figure 16
does not seem to intersect
the attractor, which is another indication that our computation is
correct.
The clockwise and counter clockwise wrapping of the manifold in the
right and left half of the attractor, respectively, cause 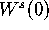 to
become tangent to a foliation leaf. This is also demonstrated in the
animations.
The algorithm adds rings to the
approximation of
to
become tangent to a foliation leaf. This is also demonstrated in the
animations.
The algorithm adds rings to the
approximation of 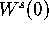 until a piece of the manifold is missed that
is necessary for the further computation. The (arclength) distance of
the outer circle, that consists of 1267 points, to the origin
is approximately 42.6, so that a
substantial part of the stable manifold was computed.
until a piece of the manifold is missed that
is necessary for the further computation. The (arclength) distance of
the outer circle, that consists of 1267 points, to the origin
is approximately 42.6, so that a
substantial part of the stable manifold was computed.
We remark that it is best to have a mesh with triangles that intersect
the leaf 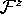 through the z-axis, because the z-axis is
invariant for the time t-map. The reason is computational: the image
of a triangle never intersects
through the z-axis, because the z-axis is
invariant for the time t-map. The reason is computational: the image
of a triangle never intersects 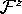 , unless the triangle
itself intersects
, unless the triangle
itself intersects 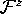 .
.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Wed Jul 2 10:51:02 1997