Abstract and Contents

The quasiperiodically forced Hénon map is defined on 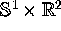, where we identify 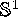with 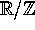. This family is studied in [Sosnovtseva et al. 1996], and it is defined as

The rotation 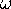must be irrational, and in practice we choose the golden mean 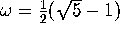. For A = 0 we get an uncoupling of the 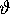-parameter, and the system is simply the Hénon map times a rigid rotation, so that fixed points of the Hénon map are circles of (5). For positive A the structure is more complicated, and as A increases, the invariant circles can become strange attractors; see [Sosnovtseva et al. 1996] for details.

We compute stable and unstable manifolds of the quasiperiodically forced Hénon map (5) for 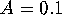, 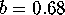and 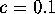. For these parameter values, the Hénon map has an attracting orbit of period 2 and two saddle points. Hence, (5) for A = 0 has two attracting periodic circles and two circles of saddle-type, whose stable and unstable manifolds are two-dimensional. For 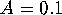the two attracting period-two circles and the two circles of saddle-type still exist and they are all normally hyperbolic. One of the circles of saddle-type lies in between the two period-two circles and the other lies far away from the attractor. We used [Osinga 1996] to compute both circles of saddle-type together with the linear approximation of their stable and unstable manifolds.

Our goal is to gain insight in the global dynamics. For this purpose we compute one branch of the unstable manifold of the circle of saddle-type that is far away from the attractor. The result is shown in Figure 11. The computation is started at 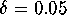away from the circle, using 50 leaves of the foliation 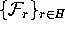where 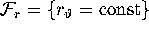. The intersections of the unstable manifold with the leaves 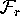are computed with an accuracy of 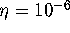and the distance between neighboring points on each leaf does not exceed 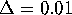. The colored bands on the manifold have width 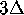. Figure 11 shows that the unstable manifold converges to the attracting period-two circles by folding; the fold is clearly seen in the enlargement of Figure 11.

There must be infinitely many folds, that lie extremly close to each other, because the manifold cannot go past the other circle of saddle-type. It may be possible to compute more folds when is taken very small. The computation was also performed with larger . The two manifolds were different only after the first fold; compare Section 4.

We also computed the stable manifold of the other circle of saddle-type. The computations were performed with the same accuracy. One branch of this manifold must intersect the folding unstable manifold of Figure 11. Figure 12 shows that there is indeed heteroclinic tangle of the two-dimensional stable and unstable manifolds. In the animations one can see how the manifolds intersect.

We computed the stable and unstable manifolds that form the heteroclinic tangle, but we did not include the other stable and unstable manifolds in the figures. For completeness we mention that the branch of the unstable manifold in Figure 12 accumulates on the unstable manifold of the other circle. This manifold connects the two period-two attracting circles. Similarly, the branch of the stable manifold in this figure accumulates on the stable manifold of the other circle.

Abstract and Contents

Written by: Bernd Krauskopf & Hinke Osinga
Created: May 27 1997 --- Last modified: Wed Jul 2 10:53:36 1997